Many algorithms are recursive in nature. When we analyze them, we get a recurrence relation for time complexity. We get running time on an input of size n as a function of n and the running time on inputs of smaller sizes. For example in Merge Sort, to sort a given array, we divide it in two halves and recursively repeat the process for the two halves. Finally we merge the results. Time complexity of Merge Sort can be written as T(n) = 2T(n/2) + cn. There are many other algorithms like Binary Search, Tower of Hanoi, etc.There are mainly four ways for solving recurrences.
Many algorithms are recursive in nature. When we analyze them, we get a recurrence relation for time complexity. We get running time on an input of size n as a function of n and the running time on inputs of smaller sizes. For example in Merge Sort, to sort a given array, we divide it in two halves and recursively repeat the process for the two halves. Finally we merge the results. Time complexity of Merge Sort can be written as T(n) = 2T(n/2) + cn. There are many other algorithms like Binary Search, Tower of Hanoi, etc.There are mainly four ways for solving recurrences.
- Substitution Method
- Iteration Method
- Recursion Tree Method
- Master Method
1. Substitution Method:
The Substitution Method Consists of two main steps:
- Guess the Solution.
- Use the mathematical induction to find the boundary condition and shows that the guess is correct.
Example1
Solve the equation by Substitution Method
Solve the equation by Substitution Method
T (n) = T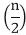 + n
+ n
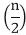 + n
+ n
We have to show that it is asymptotically bound by O (log n).











0 Comments