Recents in Beach

Matrix chain multiplication

Matrix chain multiplication (or Matrix Chain Ordering Problem, MCOP) is an optimization problem that can be solved using dynamic programming. Given a sequence of matrices, the goal is to find the most efficient way to multiply these matrices. The problem is not actually to perform the multiplications, but merely to decide the sequence of the matrix multiplications involved.
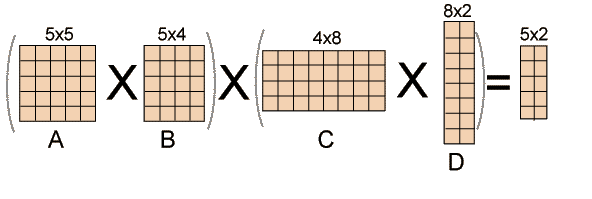
Here are many options because matrix multiplication is associative. In other words, no matter how the product is parenthesized, the result obtained will remain the same. For example, for four matrices A, B, C, and D, we would have:
((AB)C)D = ((A(BC))D) = (AB)(CD) = A((BC)D) = A(B(CD))
_config.yml
Dynamic Programming Solution :
  • Take the sequence of matrices and separate it into two subsequences.
  • Find the minimum cost of multiplying out each subsequence.
  • Add these costs together, and add in the cost of multiplying the two result matrices.
  • Do this for each possible position at which the sequence of matrices can be split, and take the minimum over all of them.
Program in C :


 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// This code implemented using Algorithm in Coremen book
 
#include<stdio.h>
#include<limits.h>
 
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
 
int MatrixChainMultiplication(int p[], int n)
{
    int m[n][n];
    int i, j, k, L, q;
 
    for (i=1; i<n; i++)
        m[i][i] = 0;    //number of multiplications are 0(zero) when there is only one matrix
 
    //Here L is chain length. It varies from length 2 to length n.
    for (L=2; L<n; L++)
    {
        for (i=1; i<n-L+1; i++)
        {
            j = i+L-1;
            m[i][j] = INT_MAX;  //assigning to maximum value
 
            for (k=i; k<=j-1; k++)
            {
                q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
                if (q < m[i][j])
                {
                    m[i][j] = q;    //if number of multiplications found less that number will be updated.
                }
            }
        }
    }
 
    return m[1][n-1];   //returning the final answer which is M[1][n]
 
}
 
int main()
{
    int n,i;
    printf("Enter number of matrices\n");
    scanf("%d",&n);
 
    n++;
 
    int arr[n];
 
    printf("Enter dimensions \n");
 
    for(i=0;i<n;i++)
    {
        printf("Enter d%d :: ",i);
        scanf("%d",&arr[i]);
    }
 
    int size = sizeof(arr)/sizeof(arr[0]);
 
    printf("Minimum number of multiplications is %d ", MatrixChainMultiplication(arr, size));
 
    return 0;
}


Output :


Post a Comment

0 Comments